音頻的測量方法
1、示波法測量頻率
(1)測周期確定頻率
可用測周期的方法,先測得信號的周期,再由信號的頻率與周期是倒數關系,求倒數得到信號的頻率。這種測量方法雖然精度不太高,但很方便,常用作頻率的粗略測量。
(2)Lissajous圖形法
1)被測頻率fy的電壓加到Y軸通道上,而把標準頻率fx的電壓加到X軸通道上,熒光屏上顯示的圖形稱為Lissajous圖形。
2)Lissajous圖形的形狀與輸入的兩個正弦信號的頻率和相位差有關,因此可以通過對圖形的分析來確定信號的頻率及相位差(Lissajous圖形法測相位差)。
Lissajous圖形,如圖1所示:
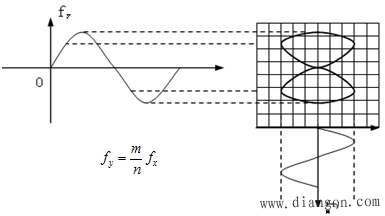
圖1 Lissajous圖形
確定m、n的數值:
Lissajous圖形應與X軸有2m個交點,與Y軸有2n個交點,所以只要從顯示的Lissajous圖形上數出這些交點,就可確定m、n的數值。
在Lissajous圖形上分別作兩條不通過圖形本身的交點,也不與圖形相切的水平線和垂直線,數出圖形與水平線的交點即為2m,與垂直線的交點為2n。
Lissajous圖形法一般適用于被測頻率和標準頻率十分穩定的低頻信號(音頻到幾兆赫范圍),而且一般要求兩頻率比Z大不超過10倍,否則圖形過于復雜而難以測準。
如果fy與fx不成比例關系,則熒光屏上顯示的圖形是不穩定的或旋轉變化的,這時還應該繼續調節標準頻率信號源,直到圖形穩定。只有當fy:fx=m:n(m,n為整數)時,熒光屏上才能顯示穩定的圖形。由于標準信號源的頻率是已知的,只要能確定比值m:n,就可算出被測信號頻率。
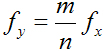
不同頻率比和不同相位差的Lissajous圖形,如圖2所示:
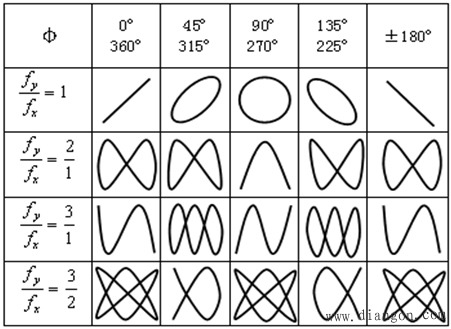
圖2 不同頻率比和不同相位差的Lissajous圖形
2、計數法測量頻率
(1)原理
計數法測量頻率,如圖3所示:
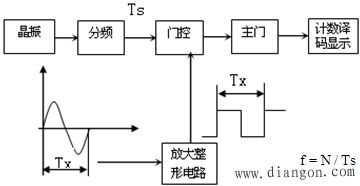
圖3 計數法測量頻率
(2)量化誤差(±1誤差)
1)產生原因
在計數時,如果主門的開啟信號與被測信號之間沒有同步鎖定關系,同一被測信號在相同的主門開啟時間內兩次測量所記錄的脈沖數N可能不一樣。
±1誤差示義圖,如圖4所示:
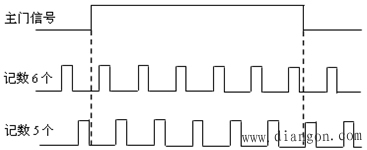
圖4 ±1誤差示義圖
2)量化誤差
量值Z大計算誤差ΔN=±1,它稱為量化誤差或±1誤差。Z大計數相對誤差的形式為
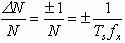
當主門控制信號Ts的誤差不能忽略,總誤差可采用分項誤差絕對值合成得到
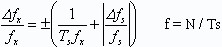
式中:Δfs/fs——標準頻率誤差,是晶振頻率的準確度
3、拍頻法
(1)拍頻法
是將被測頻率與標準頻率相比較。被測頻率fX的信號與標準頻率fS的信號同時加到一個線性元件——耳機上。
(2)如果改變頻率fS使之非常接近頻率fX時(例如兩頻率之間相差5Hz左右),就分不出兩個信號頻率(音調)上的差別了,此時視為零拍。這時只聽到一介于兩個音調之間的音調,同時,聲音的響度(振幅)隨時間作周期性變化。這種現象在聲學上稱為拍。聲音的響度變化頻率正好就是兩頻率之差|fX-fS|。當兩頻率完全相等時,合成波的幅度就不變化了。
拍頻法測量音頻的方框圖,如圖5所示:
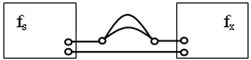
圖5 拍頻法測量音頻的方框圖
(3)數學推導
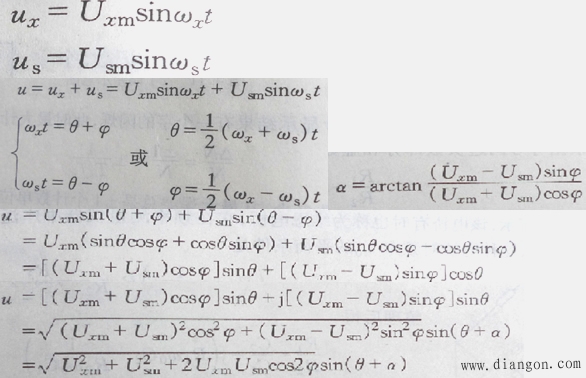

4、電橋法
(1)電橋法只用來測量音頻頻率。(高頻時寄生電感和電容對電橋的調節有很大的影響)
(2)根據電路原理的知識,我們知道,如果把一電壓加到電橋的一個對角線上,通過調節對應的元件就可以使電橋的另一對角線上的電壓為零,即電橋達到了平衡。如果電橋平衡的條件(橋臂上存在電感和電容元件)與所加電壓的頻率有關,則該電橋就可以用于測量頻率。常用的電橋法有諧振電橋、電容電橋和雙T電橋。
1)諧振電橋
首先,適當選取可變電阻R1的值,然后調節電感和電容使回路對所加電壓的頻率諧振,這樣回路的阻抗才是純電阻,才能測出被測頻率。該方法缺點是改變被測頻率Fx時,每次不僅要把回路調節到諧振,同時還要調節電阻R1,并且測量低頻時回路較笨重。
諧振電橋電路,如圖6所示:
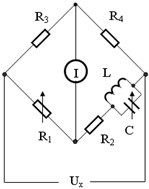
圖6 諧振電橋電路
2)電容電橋
A、可以用電阻或電容來改變電橋的頻率。
B、在被測頻率的電壓中有諧波時,就很難使電橋達到平衡。因為,電橋對基波平衡了,對諧波則不平衡。這種電橋僅適用于10KHz以下的音頻范圍。
電容電橋電路,如圖7所示:
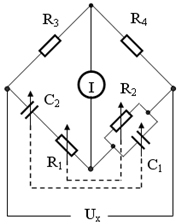
圖7 電容電橋電路
C 、數學推導
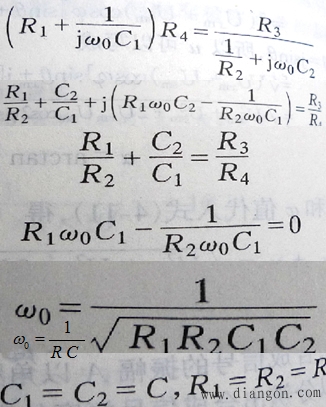
3)雙T電橋
被測頻率的信號源與指示器具有共同的接地點通過改變電阻R1和R2,來平滑調節頻率。測量頻率的誤差一般為0.5~1%。
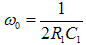
雙T電橋電路,如圖8所示:
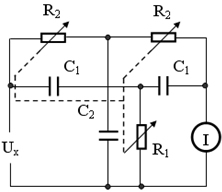
圖8雙T電橋電路
上一篇:數字高壓表原理